Know in one minute about Tetrahedral voids
R = 0.225r
|
Introduction
Tetrahedral voids and octahedral voids are the empty space that remains between the constituent particles that make up the crystal of a substance. The study of these voids is helpful in studying the structure of the compound and telling its properties. Compounds often have either ccp (cubic close-packed) or hcp (hexagonal close-packed) structures.
When atoms combine in a tetrahedral way, tetrahedral voids are formed and if they combine in an octahedral way, octahedral voids are formed.
Close packing in solids
The constituent particles that make up solids are closely packed in a regular pattern. These particles are packed in such a way that the gap between them is minimal. Generally, their packing arrangement can be understood in 3 ways. To understand this easily, we have assumed that the constituent particles are of spherical shape.
1. Close packing in one dimension
When the constituent particles of a substance are arranged one after the other in a straight line.
2. Close packing in two dimension
In two dimensions close packing, the chains of particles are arranged one after the other in a regular manner. Particles of a solid substance can be arranged in two dimensions in two ways:
Cubic close packing in two dimensions (AAA type):

Here, chains of particles are placed in such a way that the next chain is placed just above the previous chain and the consecutive spheres of each chain are together.
If the first series is of A type, then the second and subsequent series will also be of the same A type.It is proved to be the same when viewed from both horizontal and vertical angles.(image)
Hexagonal close packing in two dimensions (ABAB type):

In this type of packing, the chains of the constituent particles of the substance are arranged in such a way that the second chain is in a staggered manner from the first chain. And the particles of the second series come between the adjacent spheres of the first series.
After that, the third chain is arranged adjacent to the first chain and it comes in a staggered manner from the second chain. If the type of the first series is A, then the type of the second series is called B, and the third series which was arranged in the same way as the first series is called A type.
3. Close packing in three dimension:
In three-dimensional close packing, there are also two ways to arrange atoms:
FCC packing:
FCC (face-centered cubic ) close packing is such that each atom present in the unit cell is surrounded by twelve other elements.
In this way, packing is found in many elements, in which packing is also done well and minimum empty space is also very less.
HCP packing:
In HCP (hexagonal close packing), atoms are present at each corner of the hexagonal prism and at the center of each upper and lower face.
Both types of three-dimensional FCC and HCP packing have a packing efficiency of about 74%, which is the maximum efficiency that can be achieved in three-dimensional packing.
What are voids?
Voids can be defined as follows: When the constituent particles of solid substances are arranged in a regular order, some gaps remain between those particles, these gaps are called voids.
To understand this, we have to assume that the shape of the particles that make up the substance is like a sphere. Now we arrange these particles in a constitutive way. As seen in the image, we have placed the particles according to the AA-type arrangement (AA refers to the way the first line of spheres is made, just below it, the line of all other spheres is kept in the same way)
(Image)
The empty gap that remains between the two constituent lines of these spheres, this gap is called the void of the structure of solids in chemistry.
Types of voids
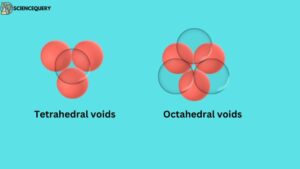
To understand voids, let us understand the three-dimensional structure. When another two-dimensional structure is placed on top of a two-dimensional structure, a three-dimensional structure is formed.
These atoms are arranged in 3D, they create two different types of gaps(voids), these voids are:
-
Tetrahedral voids
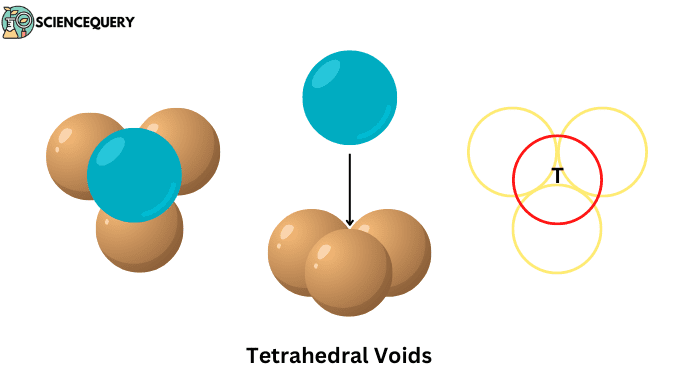
When a layer of spheres or atoms is placed on top of another layer in such a way that the adjacent atoms of the upper layer cover the gap between the atoms of the lower layer. Then the four atoms together form this empty space whose shape is triangular, this gap itself is called tetrahedral void.
-
Octahedral voids
When the second layer is placed on top of one layer of spheres or atoms in such a way that the gaps of the spheres of the second layer come just above the gaps made between the spheres of the first layer. In this way a total of six atoms join together to form a regular octahedron shape, Then the gap that is formed between these atoms is called octahedral voids.
Tetrahedral voids
When the atoms of the crystal lattice are arranged in a tetrahedral crystal system, tetrahedral voids are generated.
As the name suggests, tetrahedral voids are somehow related to the shape of tetrahedrons. Actually,
Tetrahedral voids are the interstitial empty spaces between the regular tetrahedron-shaped arranged atoms in a crystal system.
The characteristics of tetrahedral voids and how to calculate them are given as follows:
● Characteristics of tetrahedral voids:
- Are formed on the interstitial space between the four atoms or ions present on the unit cell of the crystal lattice.
- Their shape is triangular, which we can see in the middle of all four atoms.
- And their constituent atoms are arranged at the corners of a regular tetrahedron.
- The size depends on the size of the constituent atoms or ions. If the radius of the atom or ion is R and the radius of the sphere occupying the tetrahedral void is r, then the relation between them is as follows:
r = 0.225R
- Atoms that form tetrahedral voids have a coordination number of 4.
● Calculation of tetrahedral voids:
The number of tetrahedral voids present in a solid structure depends on the number of closed-packed spheres present in the unit cell of the crystal lattice.
In fact, the number of tetrahedral voids is twice the number of spheres on the lattice.
If N is the number of close-packed spheres, then
Number of Tetrahedral voids = 2N
The number thus can also be derived from such that,
“The number of tetrahedral voids formed by a sphere is equal to the coordinate number of that sphere.”
Some questions for better understanding
Example 1
An element X forms the HCP lattice, in which the Y element occupies ½ of tetrahedral voids, what is the formula of the compound by the elements X and Y?
Solution
As we know that there are a total number of Tetrahedral voids = 2 x the number of atoms of
element X
Question says,
½ tetrahedral voids are occupied by Y
So,
½ tetrahedral voids = number of atoms of element Y
By the formula:
½ tetrahedral voids = 2× ½ number of atoms of element X
½ tetrahedral voids = number of atoms of element X
Number of atoms of element Y = Number of atoms of element X
So the formula will be XY.

Example 3
A certain compound has a face-centered cubic structure with atoms of A occupying all the corner positions and atoms of B occupying all the face-centered positions. What is the total number of tetrahedral voids per unit cell?
Solution
Since,
atoms of A occupy corner of the cubic unit cell and B occupies the face center position
So, they together make the FCC structure
In FCC structure
total number of atoms = ⅛ (number of corner atoms) + ½ (Number of face-centered atoms)
Because there are 8 corners and 6 faces in a lattice, the number of atoms occupying corner(A) = 8
And number of atoms occupying faces(B) = 6
Total number of
atoms in FCC lattice(N) = ⅛ (8) + ½ (6) = 4
Number of tetrahedral voids = 2N
So,2 × 4
Therefore, it is 8
Difference between tetrahedral voids and octahedral voids
Key points |
Tetrahedral voids |
Octahedral voids |
| Definition | These are unoccupied interstitial empty spaces between the atoms or ions or molecules of the substances which have a tetrahedral crystal system. | Octahedral voids are unoccupied interstitial empty spaces between the atoms or ions or molecules of the substances which have an octahedral crystal system. |
| Shape | When the centers of atoms forming tetrahedral voids are joined, the shape formed is tetrahedron shape. | When the centers of the atoms forming the octahedral voids are joined, the octahedron shape is formed. |
| Number of forming atoms | They are formed by the combination of four atoms | They are formed by the combination of four atoms. |
| Calculation formula | If the number of close-packed spheres is N, then
The number of Tetrahedral voids= 2N |
If the number of close-packed spheres is N, then
The number of octahedral voids= N |
| Location | In fcc or ccp lattice they are found in corners | They are found in the fcc or ccp lattice at the center of the body and also at the center of the edges of the lattice. |
| Radius | The radius of tetrahedral voids is
R = 0.225r Where r is the radius of crystal-forming atoms or ions |
And radius of octahedral voids is
R = 0.414r Where r is the radius of crystal-forming atoms or ions |
| Size | They are smaller as compared to octahedral voids. | Octahedral voids are bigger as compared to tetrahedral voids |
Q&A
1. How many lattice sites of octahedral, and tetrahedral voids are contained in a hcp unit cell?
Ans. In a hexagonal close packed(hcp) unit cell there are 12 tetrahedral voids and 6 octahedral voids.
Tetrahedral voids are formed at the corners of the unit cell while octahedral voids are present at the center of faces of the unit cell.
2. How many octahedral and tetrahedral voids are occupied by all ions in γ-Al2O3?
Ans. γ-Al2O3 has a hexagonal close-packed structure, in which oxygen ions(O²⁻) occupy corner face-centered and body center sites and Al⁺³ occupies ⅔ of octahedral sites.
number of oxygen ions in an hcp lattice would be:
O²⁻ = 12(corner)× ⅙ + 2(face)× ½ + 3 (body-centered)
O²⁻ = 6
number of aluminum ions
Al⁺³ = ⅔ × 6
Al⁺³ = 4
So,
In γ-Al2O3, Al⁺³ ion occupies only 4 octahedral and 0 tetrahedral voids.
3. What is the difference between tetrahedral and octahedral voids?
Ans. The major differences are given below:
- Tetrahedral voids are unoccupied spaces in a substance by atoms or ions that have a regular tetrahedral shape. On the other hand, octahedral voids are also unoccupied spaces whose shape is like an octahedron.
- Former requires four atoms or ions to form, whereas octahedral voids with six atoms or ions form a gap between them.
4. What is the c.n. of any given sphere with respect to tetrahedral voids?
Ans. As we know, Tetrahedral voids are the triangular-shaped empty space between four atoms or ions or it can also be said that they are made up of four atoms or ions.
That is why the coordination number of tetrahedral voids is 4.
