What is the number of tetrahedral voids in the fcc lattice of a solid?
a. 2
b. 4
c. 6
d. 8
Detailed solution for Number of tetrahedral voids in fcc
The crystals of solids are formed by arranging several crystal lattices in some order. These crystal lattices are made up of very small units called unit cells. That is, the smallest unit of a solid is called a unit cell.
These unit cells are of two types; cubic unit cells and hexagonal unit cells.
In both types of unit cells, the constituent atoms or ions are arranged in various ways. These atoms are arranged in the unit cell mainly on the corner, face of the unit cell, at the center of the body, and at the center of the edge.
Due to the presence of these atoms in a certain place in the cubic unit cell and due to being arranged in a certain order, some of their types have been described:
- The primitive unit cell (simple cubic unit cell):
This type of unit cell, the constituent atoms or ions are arranged only at the corners of the unit cell.
- Face-centered cubic(fcc) unit cell:
In the fcc unit cell, the constituent atoms or ions are present at the center of the body as well as on all the faces of the unit cell.
- Body-centered cubic (bcc) unit cell:
The Bcc unit cell, the constituent atoms or ions are present at the corners of the unit cell and one atom is also present at the center of the body.
- Edge-centered cubic unit cell:
In the edge-centered cubic unit cell, the constituent atoms or ions are present at the corners of the unit cell and also in between the edges.
Face-centered cubic( fcc ) is a type of cubic closed unit cell of a crystal lattice in which one constituent atom or ion is present at every corner of the unit cell and one atom or ion is present at the center of every face.
Since every corner atom is in the middle of 8 unit cell’s corners. Hence, it shares ⅛ part of itself with each unit cell. Similarly, every face atom shares it’s half part to each unit cell Because it is present between two adjacent unit cells.
So the total number of atoms in an fcc unit cell will be:
⅛ ×8 + ½ ×6 = 4
When the atoms that make up the crystal lattice are arranged. Then some space remains empty between them, these empty spaces are called voids. These voids are of two types:
- Tetrahedral voids
- Octahedral voids
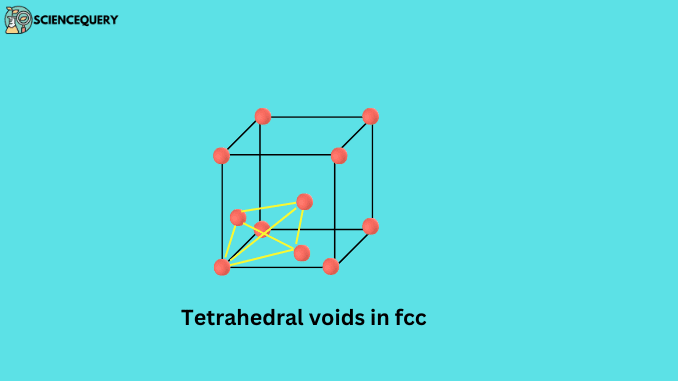
The triangular-shaped void is formed between forming atoms of the crystal lattice. When these atoms are arranged in a tetrahedral way, these voids are called tetrahedral voids.
The number of octahedral and tetrahedral voids on a unit cell can be calculated in such a way that the number of octahedral voids in the unit cell is equal to the total number of atoms present in that unit cell. And the number of tetrahedral voids is twice the number of atoms.
Number of octahedral voids = N
Number of tetrahedral voids = 2N
Since there are only 4 atoms in the bcc unit cell, the number of tetrahedral voids on it will be 2 × 4 = 8.
So the correct answer will be (d) 8.
Written By: Amber Soni
