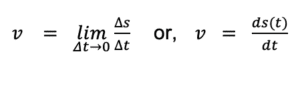Table of Contents Toggle Know in one minute about Instantaneous Velocity Velocity is a term that describes how fast something is covering a distance in a particular direction. The measurement of velocity for large differences in time is called average velocity. It is the measurement of time when the difference becomes closer to zero. The formula is It is a vector quantity and its direction is tangential to the curve followed by a particle or object. The magnitude of instantaneous velocity is called speed. It is a very important term in physics, which gives us the velocity of any object at any instant in time. The slope of the curve at any point gives the instantaneous velocity at that point.

Introduction 

Instantaneous Velocity is the velocity at a particular instant of time. For example, if the velocity of a car is 20m/s, this means that we are talking about the instantaneous velocity of that car i.e. velocity with which the car is moving at a specific point of the path.

Velocity in simple words describes how fast a particle or object can complete a distance in a particular direction. There are two types of velocity in physics.

1. Average velocity:

It is measured in total displacement upon the total time taken. Or simply

                                                                     “Average velocity is the velocity measured over a time interval.”

                                                                                                                            Or                                                                                                                                                                                                                                             “the ratio of total displacement and total time is called average velocity”

Let us understand the simple equation for Average velocity

 

2. Instantaneous velocity

If we want to calculate the velocity at a particular instant of time during the travel, for this the above formula will not work as it gives the velocity between two time periods during the journey which has a somewhat big difference.

So we use instantaneous velocity to find the velocity at that particular instant of time.

♦ Points to remember

• Time is the main defining factor between average and instantaneous velocity.
• Average velocity is calculated when the time difference is high on the other hand instantaneous velocity is determined when the time difference is only a fraction of a second.
• The main difference between them is their formula.

Let us understand the time difference with the help of a simple equation

As the name suggests, instantaneous velocity is the velocity of an instant of time.

We know the formula for average velocity and that is

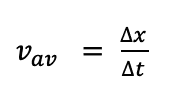
Here, the time difference could be big, but if the time difference becomes as small as 0 or <<<<<1 then this difference will become a fraction of a second i.e. ∆t→0.

To understand this let us consider an example:

The time difference in average velocity:

 

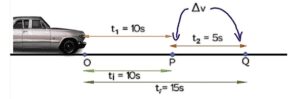
A car is moving with velocity v on a straight line, it covers OP distance in t₁ = 10s  and covers the next PQ distance in t₂ = 5s, if we have to find the velocity between points P and Q, then here time will be

tᵢ = 10s

t_f = t₁+t₂ = 10+5 =15s

so time difference for path PQ is

∆t =  t_f – tᵢ

∆t = 5s

The time difference in instantaneous velocity

 

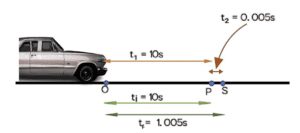
Considering the same example, the car covers OP distance in t₁ = 10s and covers the next small distance PS in t₂ = 0.005s, so the time difference will be

tᵢ = 10s (time consumed during OP)

t_f = 10.005s (time consumed during OS)

∆t = tᵢ – t_f

∆t = 0.005s

Here, the time interval is very small, almost equal to zero (∆t → 0). If we apply this time interval in the formula of average velocity obtained for such a small interval will be instantaneous velocity and it will be obtained at point P.

Definition                                              

                                       “Instantaneous velocity is average velocity when the time difference is approaching zero.”

or

                                               “Object’s velocity at a specific point of the path is called instantaneous velocity.” 

The formula of instantaneous velocity mathematically

 

Some examples to build a better understanding (1)

Difference between Average velocity and Instantaneous velocity

Key points	Average velocity	Instantaneous velocity
Definition	The ratio of total displacement and the total time taken by the body is average velocity.	Displacement of the body at a specific instant of time.
Formula
Time interval	It occurs when the time difference is large.	When the time difference is approaching zero.
Direction	The direction is in the direction of the displacement vector.	The direction of a particle is tangential at that point of its path
Uses	If we have data that is accumulated over time and the change in time is insignificant, then we use average velocity.	When data is not accumulated over time, we use instantaneous velocity.

Difference between speed and instantaneous velocity

Key points	Instantaneous Speed	Instantaneous velocity
Definition	The magnitude of instantaneous velocity is called instantaneous speed.	Displacement of the body at a specific instant of time is
Formula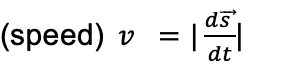
quantity	It is a scalar quantity (only has magnitude.)	It is a vector quantity (it has magnitude and direction both)
Direction	Speed doesn’t have direction.	The direction of the instantaneous velocity of a particle is tangential at that point of its path
Uses	Speedometers in bikes and cars measure the speed.	If we want the speed with the direction of the object, then we measure instantaneous velocity.

Written By: Amber Soni

References

Related topics

 

1. Define uniform circular motion with examples

2. What is instantaneous angular velocity?