Table of Contents Toggle Know in one minute about Uniform circular motion When a particle or object moves along a curved or circular path, the motion of that particle or object is called circular motion. Motion while turning a vehicle on a curved road is circular motion. There are two types of circular motion, Nonuniform circular motion Uniform circular motion When we maintain the speed of the object constant in the whole circular motion, it is called uniform circular motion.             ∆v  =  0

Introduction

Uniform circular motion is an important phenomenon that is essential for our day-to-day life. This is a type of circular motion, describing the motion of many natural things. Whenever a body moves or travels on a curved or circular path, then the motion of that body is called circular motion.

For example, as shown in the main diagram above the bike is moving in a curved or circular path.

We know that when a body is moving then it will have a velocity. And in a circular path, the body changes its direction at every instant, and because of that the direction of the velocity of the body also changes. But the magnitude of the velocity defines the types of circular motion.

There are two types of circular motion 

1. Non-uniform circular motion 

2. Uniform circular motion 

Non-uniform and Uniform circular motion

“If the speed (Magnitude of velocity) of the particle or body in a horizontal circular motion changes with respect to time, then its motion is said to be non-uniform circular motion.”

The tangent at that point of circumference where the object is present represents the direction of velocity.

By this definition, velocity is changing continuously, and because of different velocities, the path covered by the particle is also different for the same time interval.

Example

Here, the Velocity of the object at point P is v₁ and at point Q is v2. v₁ ≠ v2 so this motion is a non-uniform circular motion.

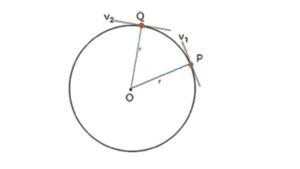
On the other hand, if the body/particle is moving on a circular path with constant speed, then its motion is considered a uniform circular motion. Here we are learning about it deeply.

Defining Uniform circular motion

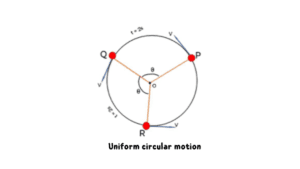
Let us consider, a ball rotating around point O on a circular path. The radius of the circular path is r. 

Here, at every point of the circular path, the magnitude of velocity is constant and that is v, and the direction is changing at every moment.

Because of the same speed at every moment, the distance covered by the particle is the same for the same time interval.

As shown in the diagram, the distance from point P to Q is the same as the distance from point Q to R in 2 seconds time intervals in both cases.

So the definition will be

When an object covers the same distance along the circumference of the circular path in the same time interval is called uniform circular motion. We can also define it as 

“If the particle/object moves in the circle with a uniform speed, we call it a uniform circular motion.”

Here, the change in speed is zero, which means

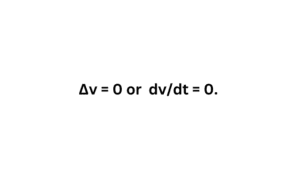
Where v is speed and it is constant.

Examples of Uniform circular motion 

1. The motion of Earth around the sun 

 Earth revolves around the sun continuously and completes one round every year, and to complete it, the earth moves the same distance (1 revolution)

If we compare this situation to the definition of uniform circular motion, we will find that the motion of the earth around the sun is uniform circular motion.

2. The motion of the tip of the second hand of watches and clocks 

Every day we see many types of watches: wristwatches, hand watches, wall clocks, etc. We can see there the tip of the second hand of these watches covers the same distance every second and their velocity is the same for every second,

This phenomenon is the uniform circular motion of the tip of the second hand of watches.

Acceleration in Uniform circular motion 

As we know, acceleration appears when there is a change in velocity. 

In the case of uniform circular motion, acceleration occurs only due to a change in the direction of velocity, and this acceleration in uniform circular motion is called Centripetal acceleration.

These are the important points that we learn from it 

•  The direction of this centripetal 

acceleration is toward the center of the circular path along the radius of the circle. 

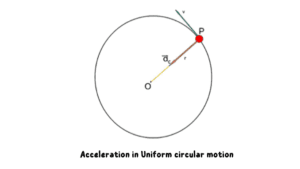
• It is also called radial acceleration because its direction is along the radius of that circular path.
• This acceleration is perpendicular to the velocity vector, so it is also called normal acceleration (aₙ)
• Formula

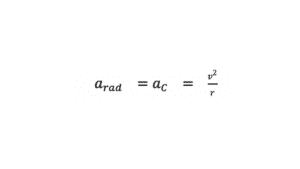
Where v is the magnitude of the linear velocity of the particle and r is the radius of the circle.

• As we know that v = ω r (ω = angular velocity of the particle at point P). So, the formula becomes

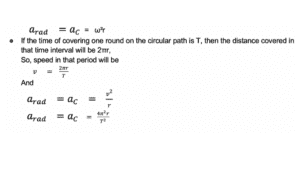
To determine the direction of centripetal acceleration, let us consider an example

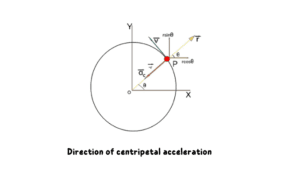
In this figure, a particle is moving along a circular path of radius r and point O is the center of the circle.

When it is at point P on the circumference, it is making angle θ from X-axis,

The radial vector r will be

 

Some examples to build a better understanding

Example 1.

An object moves at constant speed along a circular path in a horizontal XY plane, with the center at the origin. When the object is at x = 2 m, its velocity is (4 m/s). Find the object’s (a) velocity and (b) acceleration at y = 2 m.

Solution:

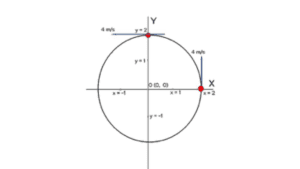
Here radius of the circle is r = 2m

and velocity at x = 2m is v = 4m/s².

It is mentioned in the question, “object moves at a constant speed”

That means it is a uniform circular motion

so (a) velocity will remain constant for y = 2 and that is

v   =    4m/s²

(b) the object is doing a uniform circular motion

That means it will have only centripetal acceleration and it is existing because of changes in the direction of velocity

Then at y = 2m, centripetal acceleration will be

(The direction of the acceleration at y = 2m will be –j

Example 2.

Find the acceleration of the moon with respect to the earth from the following data: Distance between the earth and the moon = 3.85  10⁵ km and the time taken by the moon to complete one revolution around the earth = 27.3 days.

Solution:

The moon revolves around the earth by doing uniform circular motion cause it moves with constant speed and revolves in the same period continuously

Given in the question

Distance between earth and moon = 3.85  10⁵ km or 3.85  10⁸ m

And the time taken to complete the one revolution is 27.3 days or 39,372 seconds

(27.3246060) s

The formula of centripetal acceleration is

Example 3.

A woman rides a carnival Ferris wheel at a radius of 15 m, completing five turns about its horizontal axis every minute. What are (a) the period of the motion, (b) the magnitude, (c) the direction of her centripetal acceleration at the highest point, and (d) the magnitude and (e) the direction of her centripetal acceleration at the lowest point?

Solution:

Let the speed of the Carnival is v and the radius be r

r  = 15m (given)

(a) it is given that the carnival is rotating 5 turns per minute,

As we know consumed time for 1 rotation is called the period of the motion

So, 5 rotations = 60 seconds

T = 1 rotation  = 60/5 = 12 s

(b) The magnitude of centripetal acceleration

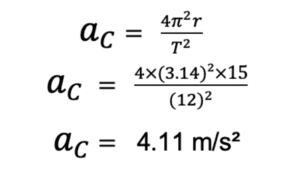
(c ) when the woman is at top of the        carnival the acceleration will direct towards the center of the carnival and it will be downwards

(d) Magnitude of centripetal a creation remains constant in a whole uniform circular motion,

That means the centripetal acceleration

at the lowest point of the carnival will be the same as the highest point of the carnival’s centripetal acceleration

And it will be

a_c = 4.11 m/s²

(e) at the lowest point of the carnival, centripetal acceleration on the woman will direct toward the center of the carnival, and that is upward,

So the direction of centripetal acceleration at the lowest point will be upward.

Example 4.

A particle of mass m is observed from an inertial frame of reference and is found to move in a circle of radius r with a uniform speed v. The centripetal force on it is

Solution:

“Inertial frame of reference means when the particle/object is observed from the ground, then the frame is called an inertial frame of reference. And in this situation, the force acts on a particle/object is called centripetal force and it directs toward the center of the circle”

We know that

Centripetal acceleration for a particle moving on a circular path

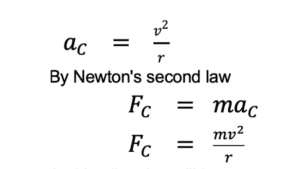
Example 5.

After a good meal at a party, you wash your hands and find that you have forgotten to bring your handkerchief. You shake your hands vigorously to remove the water as much as you can. Why is water removed in this process?

Solution:

When we try to wipe our hands with a handkerchief, we make a curved path for water particles to remove by applying tangential force on the surface of water particles,

Through this process, water particles get some linear velocity on that curved path and because of it centripetal force appears over water particles and they remove from the handkerchief.

Q&A

1. What is uniform circular motion?

Ans. When a particle or object moves along a circular path with constant speed and covers the same distance for the same time interval, then the motion of that particle/object is called uniform circular motion.

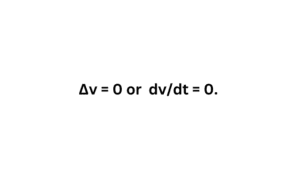
Moon revolving around the earth and earth revolving around the sun are real-life examples of uniform circular motion.

2. When is an object moves in a uniform circular motion?

Ans. When there is no external force other than the centripetal force on the object to accelerate the object moving on a circular path, then the object will not move with variable speed, so at this time, the object will move in a uniform circular motion.

That means there are two conditions

• There should be no external force on the object.
• Net acceleration should be equal to centripetal acceleration.

3. Is acceleration constant in uniform circular motion?

Ans. Yes.

4. Is velocity constant in uniform circular motion?

Ans.No it is not constant, because it changes its direction continuously, and because of it acceleration also appears.

5. A particle in uniform circular motion requires a net force acting in what direction?

Ans. It requires a net force acting toward the center of that circular path, and this force is called centripetal force.

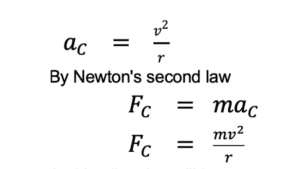
The magnitude of this force remains constant in a whole circular motion but the direction changes with the change in direction of the centripetal acceleration.

It can also be written as the above equation

Where a_c is centripetal acceleration and m is the mass of the particle.

6. In a uniform circular motion,  which of the following quantities are constant?

(a)  Angular velocity

(b)  Velocity

(c)  Speed

(d)  Angular acceleration

Ans. (C). speed

Because the magnitude of the velocity is called speed and it doesn’t change in a circular motion. In this direction of velocity changes rigorously but the magnitude of velocity remains constant, therefore speed remains constant.

Written by: Amber Soni

References

Fundamentals of physics, Halliday and Resnick, 10th edition, Jeal walker, page no. 76-77.

Concepts of physics 1, H.C.Verma, Bharti Bhawan publishers & distributors, page no. 102&112