Know in one minute about the Conservative force
|
Introduction
Conservative and non-conservative forces are the types of force that can be distinguished according to the condition of external factors. Force is a physical quantity that changes the motion of moving or still objects. In fact, conservative and non-conservative forces refer to different states of work done after applying the force.
In this article, we will read about the meaning of conservative and non-conservative forces along with their properties and examples.
Conservative force meaning
It is a type of force with some conditions, while we apply force on an object.
As the name suggests, when we are applying force on a body, So the energy of that body will be conserved.
Basically, the conservation of force and conservation of energy are associated with each other.
If we apply force on a body, it does some work. And in physics, work done is also associated with energy, thus, instead of using the term energy, we use “work done” to understand the conservative force. as we know that work done

Conservative force Definition
“Conservative force is a force when we apply it on a body moving between two points, the mechanical energy consumed by the body will be conserved.”
Kᵢ + Uᵢ = Kf + Uf
Kᵢ = initial kinetic energy
Uᵢ = initial potential energy
If = final kinetic energy
If = final potential energy
Or
Conservative force is path independent so we can say that,
“If work done between two points of a moving body depends only on the initial and final points, then the applied force will be a conservative force.”
Or
In a closed loop, the initial and final positions will be the same, so displacement would be zero.
“In a closed loop, total work done by a particle will be zero if the applied force is a conservative force.”
(total work done) WT = 0
Conservative force examples
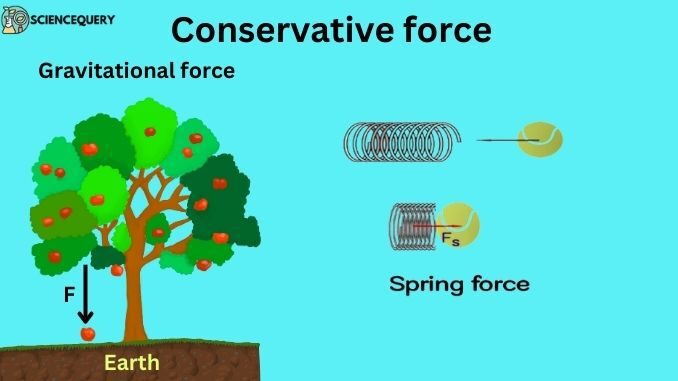
1. Gravitational force
Gravitational force or gravitational pull is a conservative force as it doesn’t depend on the path taken.
For example, if a ball of mass m is thrown upward and covers height h, initially work done by gravity will be –much, and when it comes down the work done will be +mgh
So total work done
WT = -mgh + mgh = 0
2. Coulomb force
Coulomb force or electrostatic Force is also a conservative force. Total work done by a charge in an electrostatic field to move from one point to another point does not depend on the path taken and will be zero if it comes to its initial position again by taking any path that could possible.
3. Spring forces
When an object moves by joining a spring, there is no change in its total internal energy, so the spring force is considered a conservative force.
Properties of a conservative force
- Depends only on the initial and final position of the object while applying it, it doesn’t depend on the path.
- Work done by it will be zero in a closed loop.
- The energy of the object will be conserved.
- It can do reversible work.
Work done by a conservative force
Work done by this satisfies these two conditions:
(i) If a conservative force is being applied to a body, then that body may take any path to do work, and the work done by all the paths will be equal. Work done will depend only on the initial and final position of the body.

Let a body is moving from point A to B, work done for paths (1), (2), and (3) taken to go from A to B are W1, W2, and W3
respectively, then
W1 = W2 = W3 = ∫F.dl
(ii) work done by a conservative force or against a conservative force along a closed loop is zero.

Suppose a particle goes from point A to B after applying conservative force, after that it goes back from B to A by applying the same, thus it travels in a loop. The work done in this loop will be done at zero.
WAB + WBA = 0
WI = – WII
Non-conservative force
It is the second type of force. As it is understood from the name itself that such a force due to which conservation of energy is not possible i.e. Which is defined as when energy is being lost in some way while the object is working.
Since mechanical energy (the sum of kinetic and potential energy) is lost in this, cause there is a difference between the initial and final values of work done and generated by the object,
The total work done by the object in the presence of a non-conservative force can be written as
WT = (Kᵢ + Uᵢ ) – ( Kf + Uf)
Definition of non -conservative force
Based on the previous theory, we can define it as follows
“If the force applied on the object depends on the path taken by the object as well as in initial and final position, then the applied force is called non-conservative force.”
The total work done is the difference between the initial and final mechanical energy of the object, so the energy will not be conserved while non-conservative force is applied, so we can also say that
“During the motion of an object, if energy isn’t conserved then the applied force is called non-conservative force.”
Examples of a non-conservative force
- Friction: Friction is the most important example. As we see it in many events of our daily life. If there is a friction force between two surfaces (two objects) then the deduced energy can never come back to us, nor can we use it again. This is the reason why friction force is called non-conservative force. It can be seen at many events
- The heat generated while rubbing the hands
- Repeated rubbing of the rope on the well generates heat.
- The speed of the moving pendulum automatically works because there is friction in the air.
- Viscous force: It is friction between the plates of flowing fluid, considering this concept viscous force is also a non-conservative force. The mechanical energy of the flowing fluid is not conserved in this as well, and it is also not path dependent.
Properties of a non-conservative force
- Doesn’t depend on the path.
- Here the total mechanical energy of the object is not conserved.
- The total work done in a closed loop is not zero.
Work done by a non -conservative forces
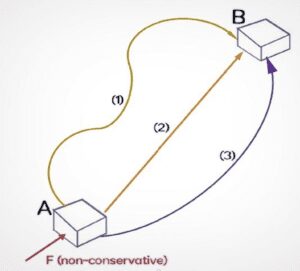
- Let a body move from point A to point B using three different paths (1), (2), and (3), if the force acting on the body is a non-conservative force. The work done by walking on all three paths are W1, W2, and W3 respectively, then
W1 ≠ W2 ≠ W3
- If the body returns from point A to B by non-conservative force or against point A, then it completes a closed loop, the work done during this time will be:
WAB + WBA ≠ 0
WI + WII ≠ 0
Difference between conservative and non-conservative force
Conservative and non-conservative forces are exactly opposite to each other. Since both forces use the object to do work and consume energy but have the property of being different from each other on several scales which are described in the table:
Key points |
Conservative force |
Non-conservative force |
| Path dependency | Total work done by conservative force does not depend on the path done, it depends only on the initial and final position. | It depends on the path set by the object |
| Energy conservation | It abides by the law of conservation of energy. | It doesn’t follow the law of conservation of energy |
| Mechanical energy | The total mechanical energy of the object will be conserved. | The total mechanical energy also changes. |
| Work recovery | The work done by this is recovered | There is no work recovery in this. |
| Examples | Gravitational force, spring force, electrostatic force, magnetic force, etc. | Friction, viscous force, etc. |
Q&A
1. Is gravity a conservative force?
Yes. Because it doesn’t depend on the path taken by the object and abides by the law of energy conservation.
2. Is spring a conservative force?
Yes as it follows the law of conservation of energy.
3. What is conservative force?
It is one of the types of force in which the total work done in a closed loop is zero. Or we can say that the work done by the force does not depend on the path. Also, total mechanical energy is conserved in it.
4. What is a non-conservative force?
It is the force by which the work done depends on the path done and the work of total mechanical energy gets destroyed along with it.
5. Is friction a conservative force?
No
Written By: Amber Soni
References
