Know in one minute about First order reactions
Rate = ln[R] = -kt + ln [R]0
|
Introduction
Reactions are processes in which two or more substances, called reactants, interact with each other to form one or more different substances, called products. These reactions have some properties that help us determine the characteristics, functioning, mechanism, and time required to complete that reaction. First order reaction is a type of chemical reaction in which the rate of the reaction depends upon the concentration of a single reactant.
The order of a reaction is an experimental quantity. It is applicable to elementary as well as complex reactions. For complex reactions, the order is given by the slowest step. The order of a reaction can be zero, negative, and even a fraction.
Depending upon the various values of the order of reactions they are of the following types :
- Zero order reaction
- First order reaction
- Second order reaction
In addition to these, there are also mixed-order reactions, where the rate law is a combination of the different orders of the reactants.
In this article, we will learn about first-order reactions in detail.
Definition
In a first-order reaction, the rate of the reaction is directly proportional to the concentration of only one reactant.
A → P
The rate law for a first-order reaction as mentioned above is:
Rate = k[A] = – d[A] / dt
Or
Rate = d[A] / [A] = – kdt
[A] in the equation denotes the concentration of the reactant.
Equations and Diagrams
To study the characteristics of a first-order reaction there are certain equations that depend upon the concentration, partial pressure (for reaction in gaseous form), etc.
Integrated rate equation
We know that,
Rate = d[R] / R] = – k dt
On integrating the equation we get,
ln [R] = -kt + I
Where I is the integration constant and its value can be determined by –
At, t = 0 R = [R]0, where [R]0 is the initial concentration of reactant.
Therefore, ln [R]0 = 0 + I (since t = 0 )
ln [R]0 = I
Hence, the equation now becomes , ln[R] = -kt + ln [R]0
Now with the equation given above, we can calculate another parameter which is known as the rate constant, the method is given below –
On rearranging the equation we will get
ln [R] / [R]o = – kt
Or k = 1/t ln [R] / [R]o
At the time t1 , ln [R]1 = – kt1 + ln [R]o
At time t2 , ln [R]2 = – kt2 + ln [R]o
Where [R]1 and [R]2 are the concentrations of the reactants at the time t1 and t2 respectively.
Subtracting these two equations, we get
ln [R]1 – ln [R]2 = – kt1 – (- kt2)
ln [R]1 / [R]2 = k (t2 – t1)
k = 1/(t2 – t1) ln [R]1 / [R]2
So, with the help of the above equation, we can calculate the rate constant of any first-order reaction.
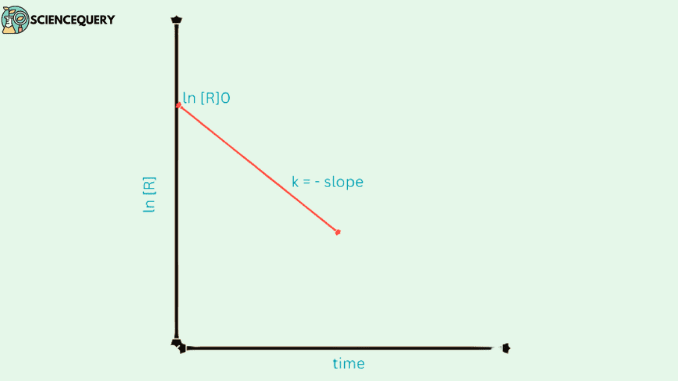
Graphs related to the first-order reaction :
Before plotting the graphs let us take the equation
ln [R] / [R]o = – kt
Comparing the equation with y = mx + c, if we plot ln [R] against t we get a straight line with slope = – k and intercept equal to ln [R]o
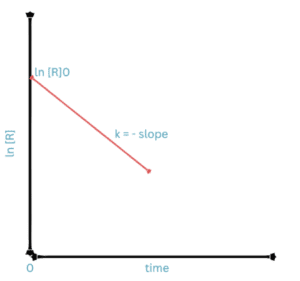
We can also write the rate equation for the first order in the form
k = (2.303 / t) log [R]o / [R]
This equation is in the log to the base 10 form.
log [R]o / [R] = kt / 2.303
If we plot a graph between log [R]o / [R] vs t we get a straight line passing from the origin with slope = k/2.303
Examples
1. Radioactive decay
The decay of radioactive isotopes is a first-order reaction because the rate of decay is proportional to the number of radioactive atoms present at any given time.
146C → 147N + 0-1e
2. Hydrolysis of esters
The hydrolysis of esters to form alcohols and carboxylic acids is a first-order reaction, as the rate of hydrolysis is proportional to the concentration of the ester.
RCOOR’ + H2O → RCOOH + R’OH
CH3COOC2H5 + H2O → CH3COOH + C2H5OH
3. Decomposition of hydrogen peroxide
The decomposition of hydrogen peroxide into water and oxygen is also a first-order reaction. The rate of decomposition is proportional to the concentration of hydrogen peroxide.
2 H2O2 → 2 H2O + O2
4. Isomerization reactions
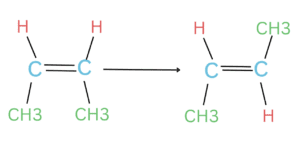
Isomerization is a chemical reaction in which a molecule is transformed into another molecule with the same molecular formula but a different arrangement of atoms. The rate of isomerization is proportional to the concentration of the starting molecule.
5. Substitution reactions
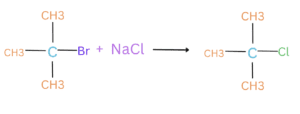
Many substitution reactions, such as the substitution of a halogen atom in an alkyl halide, are first-order reactions. The rate of substitution is proportional to the concentration of the starting molecule.
Sample Problems
1. A first-order reaction is found to have a rate constant, k= 6.93* 10-14 s-1. Find the half-life of the reaction.
Ans. Half-life for a first-order reaction is
t1/2 = 0.693/ k
t1/2 = 0.693 / (6.93*10-14 s-1)
Ans. t1/2 = 1013 sec
2. Show that in a first-order reaction, the time required for completion of 70% is 1.7 times of half-life (t1/2) of the reaction.
Ans. When reaction is 70% completed, [R]n = [R]0 – 0.7[R]0
k = (2.303/t)* log [R]o / [R]
k = (2.303/t)* log [R]o / [R]0 – 0.7[R]0
k = (2.303/t) log(1/0.3)
k = 1.202/t
t = 1.202/k
For half-life of the reaction
t1/2 = 0.693/k
Ans. t / t1/2 = 1.7
Difference between First order and second-order reactions
First order reactions |
Second order reactions |
| The rate of reaction is proportional to the concentration of only one reactant. | Rate depends upon the product of the concentration of two reactants or the square of single reactants. |
| Rate = k[A] | Rate = k[A] [B] |
| Half-life is independent of the initial concentration of the reactants. | The half-life of second-order reactions depends upon the concentration of the reactants. |
| Integrated rate equation
= ln[R] = -kt + ln [R]0 |
Integrated rate equation
= 1/[R] = kt + 1/[R]0 |
| Examples: Radioactive decay, hydrolysis of esters | Examples: acid-base neutralization reactions |
Q&A
1. How do the half-lives of first-order and second-order reactions differ?
Ans: Half-life is the time taken to complete a reaction up to an extent that the concentration of reactant decreases to half of its initial value.
For a first-order reaction half life does not depends upon the initial concentration of the reactants. t1/2 = 0.693 / k
While in a second order reaction half depends on the concentration of the reactants as t1/2 = 1 / (k [A]0)
2. How to determine first and second order reactions?
Ans: In order to classify a reaction into first order or second order we should :
- Find the rate-determining step of the reaction.
- Find the sum of stoichiometric coefficients of the reactants.
- If it comes out to be 1 then the reaction is first order reaction.
- While if we get the value of the order of reaction as 2 then it is a second-order reaction.
Written By: Bharat Awasthi
