Introduction

When there is a change in the velocity of the moving particle, a quantity called acceleration is obtained, based on which angular acceleration has also come into existence. The formula for angular acceleration is

a. Average angular acceleration:  α _{av =} Δω / Δt

b. Instantaneous angular acceleration: α = dω/dt

Angular acceleration is the concept where we learn about how much a particle is moving along a circular path varying its angular velocity. It is a time-varying quantity so it is also defined as the time rate of change in angular velocity called angular acceleration. It is denoted by α. Just like velocity, acceleration, speed, and other quantities, it can also be understood in two ways:

• Average angular acceleration
• Instantaneous angular acceleration

Average angular acceleration

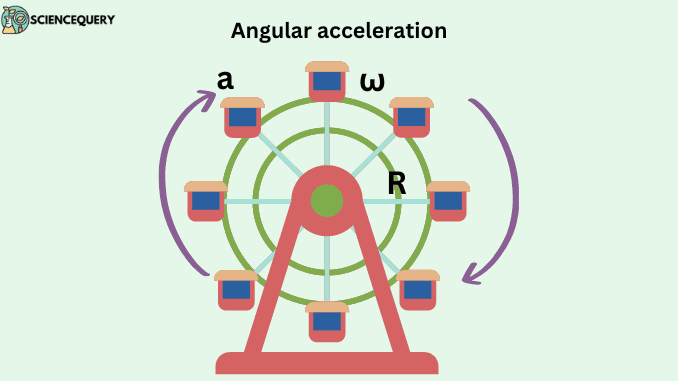
As shown in the diagram, if a particle or object is moving along a circular path, the angular velocity at point a is ω₁ and for b it is ω₂, the angular acceleration between these two points will be called average angular acceleration. So

Average angular acceleration can be defined as:

“The time rate of change in angular velocity between two points is called average angular acceleration.”

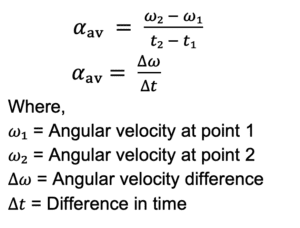
Instantaneous angular acceleration

“At any particular point in the circular path, the angular acceleration is called instantaneous angular acceleration.” According to the diagram, If we want angular acceleration of the object at a particular point p, then we use the formula of instantaneous angular acceleration

α = dω/dt

It is also called normal angular acceleration. Because normally consider it as angular acceleration.

Unit, dimensional formula, and direction of angular acceleration

It is a pseudo vector quantity, which has direction and magnitude but the direction isn’t the same as the direction of a moving particle.

Unit:

The formula says that, α = dω/dt

The unit of angular velocity is  radian/ second and we got angular acceleration by dividing it by time, so radian / Second²

Dimensional formula:

The dimensional formula is [M⁰L⁰T⁻²]

Direction:

Angular acceleration is the axial vector and its direction is the same as the angular velocity.

Using right hand-thumb rule, we can find the direction of angular acceleration,

When we rotate our right hand’s fingers along the direction of the particle’s movement, then the thumb represents the direction of angular acceleration.

1. The upward Thumb represents the Anti-clockwise direction.
2. The downward Thumb represents the Clockwise direction.

The formula for angular acceleration

Derivation of the relation between angular acceleration and linear acceleration

Some examples for better understanding

1. Merry-go-round: when we ride on a merry-go-round, initially swingers speed up on that wheel of the merry-go-round. Actually, a swinger gives torque by his physical strength and it gives angular acceleration which speeds up the ride, and angular velocity increases.

2. Earth revolves around the sun: while revolving around the sun in an elliptical orbit, Earth passes through two important points whose names are Apogee and Perigee, so when Earth reaches the point farthest to the sun called Apogee and when it comes

• nearest the point is called Perigee. Because of the relation between Angular velocity and orbital radius

ω ∝ 1 / r_e

so, because of this angular velocity changes rigorously and angular acceleration appears.

3. Car’s wheel: when we accelerate the car every particle of the wheel of the car gets angular acceleration, so because of its angular velocity increases and the linear velocity of the car increases as well.

How to approach numerically

Example 1.

A particle is moving along a circular path of radius r. angular velocity is changing with time in such a way that ω =  2t² – 6t +1, where t is time in seconds. Calculate the following:

(i) Average angular acceleration between t = 0.5 min to t = 1 min

(ii) instantaneous angular acceleration at t = 0.3 min

Solution:

Given: ω  =  2t² – 6t +1

(i) t₁= 0.5 min or 30s     t₂ = 1 min or 60s

so

ω₁ = ω_t=30 = 2 x 30² – 6 x 30 + 1

So, ω₁ = 1621 rad/sec

ω₂  = ω_t=60 = 2×60² – 6×60 + 1

ω₂ = 6841 rad/sec

so average angular acceleration will be

Q&A

1. How to find angular acceleration?

Variations in angular velocity are the cause of the generation of angular acceleration for any rotating or spinning object. If something is rotating and angular velocity is also changing rigorously there we will find angular acceleration. Thus we can say that if angular velocity is a time-dependent function, angular acceleration will exist.

2. How to calculate angular acceleration?

If the time difference between two points is larger then we will use the average angular acceleration formula

α _{av =} Δω / Δt

If we want to find angular acceleration at a particular Instant of time then we will use the instantaneous angular acceleration formula

α = dω/dt

3. What is angular acceleration?

It is the time rate of change in angular velocity.

4. How to find angular acceleration from angular velocity?

Change in the angular velocity with respect to time gives angular acceleration.

Written By: Amber Soni

References