Introduction
The total number of tetrahedral voids in bcc is 4.
Let us see how to find out
- In a body centered cubic(bcc) structure, there are a total of 2 atoms present in a cubic lattice.
- The number of tetrahedral voids in any lattice is 2N, where N represents the number of atoms.
- So, in bcc, there is a total of 2×2 = 4 tetrahedral voids present.
Let us deep dive into this query if you want to explore more
The crystals of solids are formed by arranging several crystal lattices in some order. These crystal lattices are made up of very small units called unit cells. That is, the smallest unit of a solid is called a unit cell.
These unit cells are of two types; cubic unit cells and hexagonal unit cells.
In both types of unit cells, the constituent atoms or ions are arranged in various ways. These atoms are arranged in the unit cell mainly on the corner. The face of the unit cell, at the center of the body, and at the center of the edge.
Due to the arrangement of atoms, they are divided into the following:
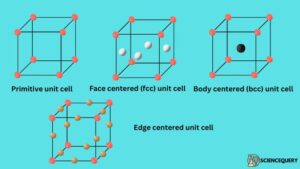
1. Primitive unit cell (simple cubic unit cell)
In this type of unit cell, the constituent atoms or ions are arranged only at the corners of the unit cell.
2. Face centered cubic(fcc) unit cell
In fcc unit cell, the constituent atoms or ions are present at the center of the body as well as on all the faces.
3. Body centered cubic (bcc) unit cell
In Bcc unit cell, the constituent atoms or ions are present at the corners of the unit cell. And one atom is also present at the center of the body.
4. Edge centered cubic unit cell
In edge centered cubic unit cell, the constituent atoms or ions are present at the corners of the unit cell and also in between the edges.
Body centered cubic(bcc) is a type of cubic close-packed unit cell of a crystal In which one constituent atom or ion is present at every corner of the unit cell of the crystal lattice and one atom or ion is present at the center of the unit cell body.
For those atoms which are at the corner of the cubic unit cell, each atom shares only 1/8th of its part with one of the adjacent cells, that is, each atom is connected to 8 unit cells.
Since there are 8 corners in a cubic unit cell, the number of atoms present in the bcc structure will be:
8 × ⅛ + 1 = 2
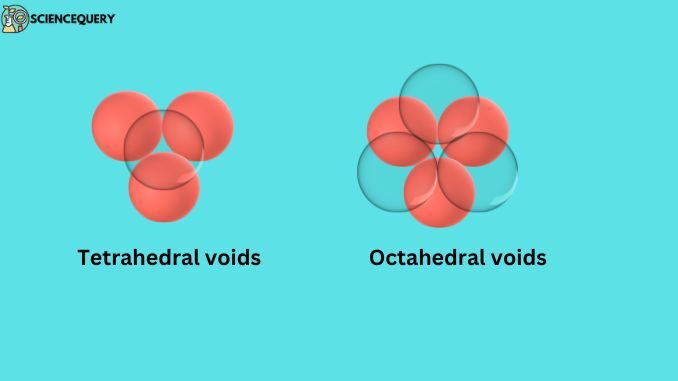
When the atoms that make up the crystal lattice are arranged, then some space remains empty between them, these empty spaces are called voids. These voids are of two types:
- Tetrahedral voids
- Octahedral voids
The triangular-shaped void is formed between forming atoms of crystal lattice when these atoms are arranged in a tetrahedral way, these voids are called tetrahedral voids.
The number of octahedral voids in the unit cell is equal to the total number of atoms present in that unit cell, and the number of tetrahedral voids is twice the number of atoms.
Number of octahedral voids = N
Number of tetrahedral voids = 2N
Since there are only 2 atoms in the bcc unit cell, the number of tetrahedral voids on it will be 2 × 2 = 4.
Written By: Amber Soni
