
Rotational motion: Introduction
Rotational means anything that rotates and any kind of motion of a body is identified by the change in position. Therefore, rotational motion refers to anything spinning or moving in a circular path. Here we will discuss the rotational motion, but first, we are going to define some of the important physical phenomena or things that are more important to create rotational motion. So these are as follows
1.System of particle
An extended body consists of a system of particles which means it is formed of a collection of particles that are interconnected with each other.
2. What is an extended body?
The kind of object that has a particular length, width, and height. Or we can say these bodies are defined by dimensions. Such a type of body is also denoted by a rigid body. As it has a specific shape and size and is denoted as a distribution of small mass elements.
Liquid and gas are not extended bodies as they have no specific shape and size. So naturally, it has no dimension therefore they have no system of particles.
3. What is a rigid body?
Solid objects have two parts namely rigid body and non-rigid body
- Rigid Body
A rigid body has a specific shape and size. The system of particles of these bodies does not change its shape by an external force. And the distance between the particles does not change with respect to time. Nothing in the universe is perfectly rigid.
Metal rods and cricket balls are examples of rigid bodies.
- Non-rigid body
It has no specific size and shape. The system of particles of these bodies changes its shape by external force thus the distance between particles is changed.
Elastic and plastic are examples of non-rigid bodies.
3. Types of motion of Rigid bodies
The rigid body has three types of motions. These are
- Pure transitional motion
- Pure rotational motion
- Combined transitional and rotational motions.
Here in this article, we are going to discuss the pure rotational motion of rigid bodies.
Why are we using a rigid body for rotational motion?
We used rigid bodies for rotational motion because objects can not be treated as particles when showing rotational motion. Since different particles of objects move with different velocities and accelerations. Therefore it is necessary to treat the object as a system of particles. Because all the particles of a system of particles can move with the same angular acceleration and angular velocities. The only extended body has a system of particles and a rigid body is a model of an extended body. So we used a rigid body for rotational motion.
Let us know about rotational motion
Rotational motion: Definition
The motion of a body along a fixed axis is called rotational motion.
The rotation motion of an object has an imaginary definite straight line called the rotation axis and the geometry plane through which the rotational motion is called a rotational plane. The rotational axis is perpendicular to the rotational plane. All celestial bodies like planets and stars etc. rotate about their own axis.
Examples of rotational motions
- The motion of the earth and other planets about their respective axis is an example of rotational motion.
- Spinning top is one example of rotational motion.
- The minute, hour, and second hand of a clock rotate in a circular direction keeping the pinpoint as the center of the axis of the rotation. Hence the hands of the clock are said to be in rotatory motion.
- Merry-go-round is another example of rotational motion.
What is circular motion?
Circular motion is a movement of an object along the circumference of a circle, that is when an object rotates in a circular path then we call that motion a rotational motion.
Example: a girl whirls a stone tied by a string. The motion of the stone is an example of circular motion.
Are rotational motion and a circular motion the same?
No rotational motion and circular motion are not same because
- In a circular motion, the object moves in a circle. Example: Wall of death game is one of the most common examples of circular motion.
- In a rotational motion, all the particles move about a fixed axis of rotation. Example merry-go-round is one of the best examples of rotational motion.
What is angular displacement?
Angular displacement is defined as “the angle of radians”. It is the angle of movement of a body in a circular path. It is denoted by ‘𝜽’.
What is angular velocity?
Angular velocity is the rate of velocity at which an object or a particle is rotated around a center or a specific point in a given time period. Angular velocity is denoted by ‘𝛚’.
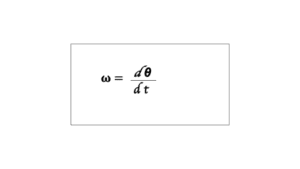
Where d is the angular displacement
dt is a change of time and its unit is radians per second (rad./s).
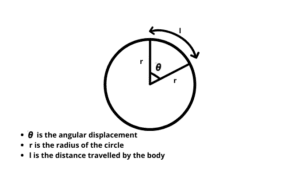
Therefore, the distance traveled by an object around the circumference of a circle divided by its radius will be its displacement.
Relation between angular displacement and angular acceleration and angular velocity
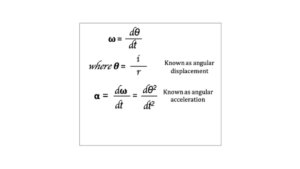
𝛚 is known as angular velocity
θ is known as angular displacement
α is known as angular acceleration
Average angular velocity
The average angular velocity of a rotating rigid body is the ratio of angular displacement to time interval.

Instantaneous angular velocity
The instantaneous angular velocity is defined as the limit of the average angular velocity as the time interval approaches zero.
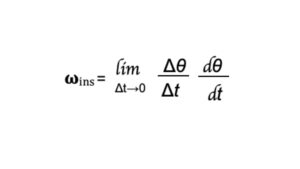
What is angular acceleration?
It is the rate of change of angular velocity.
So the simple way to say that is “How much angular velocity on an object changes every second or per second ”. This change in the angular velocity per second is called angular acceleration. It is denoted by α. Therefore the formula is
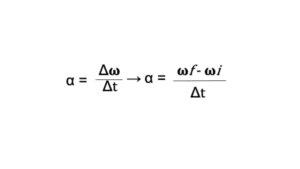
Here, 𝝎f = Final angular velocity
𝛚i = Initial angular velocity
t= time
The S.I. unit of angular velocity is rad/sec2
Moment of Inertia
The moment of inertia or rotational inertia of a body about a given axis of rotation is defined as the sum of the product of the mass of its particles and the square of the distance from the axis of rotation.
It is denoted by ‘I’
Therefore, I = m1r12 + m2r22 + m3r32 + ………mnrn2
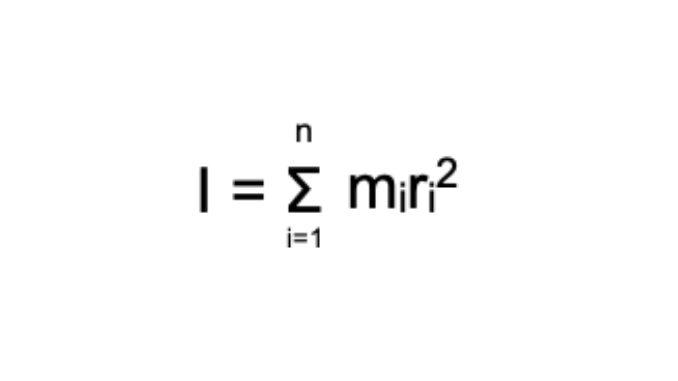
Where, r1 …………m1
r2 …………m2
r3 …………m3
r4 …………m4
r5 …………m5
Axis of rotation = r
S.I. unit = Kgm2
CGS unit = gcm2
Physical significance of M.I.
We know, in linear motion the property of a body to oppose the change of its state of linear motion is called inertia. As the mass of a body increases, its inertia also increases.
Similarly, in a rotational motion, a body has the property to oppose the change of its state of rotational motion. This property is called the moment of inertia.
Angular momentum
Angular momentum is the rotational equivalent of linear momentum. We know linear momentum equals the product of mass and velocity. So, angular momentum equals the product of angular mass (that is, a moment of inertia) and angular velocity.
Angular momentum = Moment of inertia X Angular velocity
L = I X 𝝎
Torque
Torque is the measure of the force that can cause an object to rotate about an axis.
The basic formula is
τ = F X r
τ = rF sinθ
Where Torque is represented by the Greek letter ‘tau’ (τ)
Force is represented by ‘F’
Radius is represented by ‘r’
Where, r = Position vector of the point on which force is applied or the distance measured from the axis of rotation to where the force is applied
F = magnitude of the force
θ = angle between r and F
Torque is the product of vector quantity and SI unit is = (Newton.Meter)
Rotational Kinematics
Kinematics is the description of motion. The Kinematics of rotational motion describes the relationship among rotation angle, angular velocity, angular acceleration, and time. Let us start by finding an equation relating 𝛚, α, and t.
At first, we recall a kinematic equation for translation, motion
v = v0 + at (a is constant)
Here, v is velocity
v0 is the initial velocity
a is acceleration
t is time
Now, let us substitute, v = 𝛚 and v0 = 𝛚0 into the linear equation above
𝛚 = 𝛚0 + at (a = constant)
Where, 𝛚 = angular velocity
𝛚0 = Initial angular velocity
a = angular acceleration
t = time
Thus,we can derive the following four rotational kinematic equations from the kinematic equation of translation motion.
| Rotational | Translation | a is constant |
| θ= 𝛚t | x = vt | |
| 𝛚 = 𝛚0 + at | v = v0 + at | |
| θ = 𝛚0t + ½ αt2 | x = v0t + ½ at2 | |
| 𝛚2 = 𝛚02 + 2 aθ | v2 = v02 + 2ax |
In these equations,
v0, 𝛚0 denotes the initial values, and the average angular velocity 𝛚, and average velocity v are defined as follows
𝛚 = 𝛚0 + 𝛚 / 2 and v = v0 + v / 2
These equations can solve any rotational or translational kinematics problem.
Types of rotational motion
- Pure rotation example = Rotation of ceiling fan
- Combined translation and rotation example = Rolling of wheels
- Rotation about an axis in the rotation example = the earth is moving in its orbit around the sun and rotating on its own axis at all times.
Another name of rotation is revolution
Q&A
1. What is rotational motion?
Rotational motion can be defined as the motion of an object around a circular path, in a fixed orbit.
2. What is the quantity used to measure an object’s resistance to change in rotational motion?
The moment of inertia is the quantity used to measure an object’s resistance to change in rotational motion.
3. Which is the best example of rotational motion?
The moment of spinning top is the best example of rotational motion.
4. What is the example of an object that first has rotational motion and then has linear motion?
Wheels of vehicle’s motion are the example of an object that first has rotational motion and then has linear motion
Written By: Barsha Bharati
